Assessing Formal Written Ability in Mathematics
¶ 1 Leave a comment on paragraph 1 0
¶ 2 Leave a comment on paragraph 2 0 Abstract
¶ 3 Leave a comment on paragraph 3 1 With demands to include literacy mathematics lessons from Ofsted it becomes desirable to ask what is mathematical literacy and how can we assess whether students are mathematically literate. This paper reports on a study which is aimed at addressing these questions with regards to mathematical writing. We compare the mathematical writing of small group of A-Level students to the writing style of academic mathematics (i.e. research articles, undergraduate texts etc.). We seek to understand the similarities and differences of the students’ writing style to that of academic mathematics. In doing so we also look at the quality of students formal mathematical writing. To do this we construct a rubric and grading system which measures how well students’ incorporate certain characteristics of academic mathematical writing. The characteristics in the rubric are gleaned from literary and linguistic analysis of academic mathematics literature as well as advice from professional mathematicians as to what constitutes good written mathematics. As such, the rubric tries to capture what mathematical writing is. It is found that while the students in the study use voicing techniques and formality expected in academic mathematics, their writing tends to lack cohesion and narrative of academic text. Indeed they tend to write algebraic content and descriptive content in separate blocks. At the end of the paper we discuss the implications of the findings for further research and mathematics education.
¶ 4 Leave a comment on paragraph 4 0
¶ 5 Leave a comment on paragraph 5 0 Keywords: mathematics, extended writing, literacy, assessment, linguistics
¶ 6 Leave a comment on paragraph 6 0
- ¶ 7 Leave a comment on paragraph 7 0
- Introduction
¶ 8 Leave a comment on paragraph 8 1 Over the past decade there has been an increased focus on literacy across the curriculum with Ofsted requiring each subject to include reading and writing within their teaching (Ofsted, 2013). As well as attempting to boost basic literacy, Ofsted are hoping to improve students’ ability to interpret various different kinds of information and communicate their thoughts meaningfully. This thought is echoed by various educational theorists (Lave & Wenger, 1991) who believe proficiency with the style of language used in a subject is important for the students’ participation with the academic community of that subject. The implication of all this is that a mathematics student should be encouraged to write mathematics in a way that is clear, coherent and in a way that is consistent with the style of writing in mathematics. However this raises the question, “what is the mathematical style of writing?” Following this, another natural question arises, “how capable our pupils of writing in that style?” These are non-trivial questions in mathematics education since, traditionally, extended writing has been sparse in mathematics classrooms, with most writing consisting of number of or symbolic manipulations (Baroody & Ginsburg, 1990; Nardi & Steward, 2003). A very real factor for this may be a lack of understanding among educators of what mathematical writing is.
¶ 9 Leave a comment on paragraph 9 2 The quality of students’ mathematical writing has been considered by Santos and Semana (2014). However, their focus was on the clarity of students’ mathematical writing. They do not investigate how well students’ written work converges accepted form of academic mathematical writing. The present work is dedicated addressing this issue. The study provides a rubric consisting the stylistic features found in mathematical writing. These qualities shall be distilled from literary and linguistic analyses of mathematical texts. However, since such analyses are scarce and they do not necessarily reveal what effective mathematical communication is, we shall also consult writing guides from research mathematicians on what makes good written mathematics. An assessment method is designed to go with this rubric which we shall use to assess the written work of small group of year 13 students. The students’ texts will be from single writing task. Hence, no general conclusions will be drawn from this study but at the end of the paper we shall discuss the implications of the findings of this study for research.
¶ 10 Leave a comment on paragraph 10 1 It should be clarified the style of writing being investigated here is formal in style. Hence, we it would not be appropriate to assess students’ informal mathematical writing (such as maths journals) using the techniques presented here.
¶ 11 Leave a comment on paragraph 11 0
- ¶ 12 Leave a comment on paragraph 12 0
- What is Mathematical Writing? A Literature Review
¶ 13 Leave a comment on paragraph 13 0 As one would expect, mathematical writing (and mathematical communication as a whole) has many facets to it. However, we can roughly categorise these characteristics into two groups; linguistic characteristics and structural ones. We shall address these two categories in that order.
2.1 Linguistic Aspects: The Mathematical language
¶ 14 Leave a comment on paragraph 14 1 The usage of language in mathematics has some very pronounced characteristics, some of which are unique to the subject. For this reason some have dubbed it the ‘language of mathematics’ (Morgan, 1998). We outline the key linguistic characteristics of the language of mathematics in this section. For the purposes of the following discussing we shall consider mathematics written in English.
2.1.1 Symbols
¶ 15 Leave a comment on paragraph 15 0 Syntax and the nature of the alphabet used clearly form an important part of any language. This takes on a particularly special role in mathematical discourse which uses a multitude of symbols outside of the English alphabet. So much so that Ervynck (1992) even characterised mathematical language purely by the symbol system used embedded within a meta-language. Similarly Kane defines “mathematical English” to be “a hybrid language … composed of ordinary english comingled with various brands of highly stylized formal symbol systems” (1967, p. 296). Kane explains that these formal symbol systems indeed have their own grammar i.e. rules for syntax and their semantics are derived from the context.
2.1.1.1 Embedding Symbols: Good use of Strings of Symbols
¶ 16 Leave a comment on paragraph 16 0 When writing symbolic content, mathematicians have expressed that care needs to be taken when embedding symbolic components of written mathematics into the text (Knuth, et al., 1989; Steenrod, 1973). Knuth and colleagues highlight that this symbolic component is a component of a general language being used in the text. Hence, they encourage writers to embed the symbolic statements within the natural langauge. This means, for example, avoiding starting a sentence with a symbol e.g. “ has distinct zeros”. A better sentence would be “The polynomial has distinct zeros”. Similarly, Knuth advises separating formulae with words. So instead of “Consider ” he advises “Consider , where ”.
2.1.2 Mathematical Register
¶ 17 Leave a comment on paragraph 17 0 Morgan (1998) criticised Kane and Evrynk’s characterisation of the mathematical language for not appreciating that “the non-symbolic ‘ordinary’ component also has specifically mathematical aspects” (Morgan, 1998, p. 10). Much like other technical subjects such as science and engineering, precise specialist vocabulary plays a large part in the communication of mathematics. Upon this observation, Halliday (1975) introduced what he called the mathematical register, a notion elaborated on by Pimm (1987). Halliday describes a register as “set of meanings that is appropriate to the particular function of the language, together with the words and structures which express these meanings” (Halliday, 1975, p. 65). The meanings in the mathematical register are extremely strict and can differ considerably from the meaning in natural language (Pimm, 1987, p. 78). For instance, the word ‘group’ in mathematics stands for a particular kind of algebraic structure.
2.1.3 Presence of Author and the Audience
¶ 18 Leave a comment on paragraph 18 1 In any piece of writing, the way in which an author refers to his or herself and the manner in which they refer to the audience is highly dependent on the purpose of the piece. In what we are studying here, which is formal technical writing, the style of writing is impersonal and hence, it is expected that the author and the audience are kept a certain distance from the content. This aspect springs forth from the practice of mathematics (i.e. what mathematicians do) which is key aspect of determining the discourse style (Bhatia, 1993; Gee, 2011). In mathematical texts the author is not trying to rely personal accounts but rather, establish absolute truths using deductive logic. Thus, the writing style tends to heavily detach human agency from content of the discourse.
¶ 19 Leave a comment on paragraph 19 0 In view of this, the use of the pronoun ‘I’ is generally avoided in mathematical writing (Knuth, 1985). By far the most common personal pronoun used in mathematics the impersonal ‘we’ (Knuth, 1985; Higham, 1998; Morgan, 1998). Gillman (1987) advises authors use we as ‘you and the reader’. Notice that this is somewhat personal. However, it does manage to retain the impersonal tone sought after by not specifying the reader and thereby making the action associated with the we independent of the reader or author.
¶ 20 Leave a comment on paragraph 20 0 There are other grammatical constructs used in technical writing that further engender the impersonal style required such as nominalisations (Halliday & Martin, 1993). These are nouns created from adjectives or verbs. For example, “recommendation” is the nominalisation of the verb “recommend”. Nominalisations are common in scientific disciplines and those formed from verbs tend to be particularly common in mathematics (Morgan, 1998). For example, Pillay and Ziegler choose to write “the inclusion” rather than “including” when stating, “The inclusions of and in give inclusions , and ” (2003, p. 584).
¶ 21 Leave a comment on paragraph 21 0 Like nominalisations, the passive voice is also used in science and mathematics alike to distance the author and reader (Strube, 1989; Morgan, 1998). A sentence is in the passive voice if the subject of the sentence is acted on by the verb. For example, the sentence “It is shown that is irrational” is in the passive voice whereas “I show that is irrational” has an active voice. As with scientific writing, various instructors of mathematical writing call for caution with the passive voice arguing that it can lead to awkward phrasing (Higham, 1998; Knuth, et al., 1989; Krantz, 1996). For instance, the active variant “we show that is irrational” reads more fluidly the passive version above. However, both Higham and Krantz claim that the passive voice does have a place in mathematical writing since it can add variety to the text and direct attention to the subject of the action where required.
¶ 22 Leave a comment on paragraph 22 1 A form of engagement with the audience which maybe unique to mathematics is the use of the imperative (Morgan, 1998). The requests of let, suppose, define etc. are frequently used in mathematics (e.g. “Let A be a set”) and they enjoin the audience to make them participants in the process of mathematics thinking place.
2.2 Structure
¶ 23 Leave a comment on paragraph 23 0 So far we have considered how terms are phrased in mathematical writing. We now consider how such statements are woven to make paragraphs and the text as a whole. Halmos (1975) claims that the structure of a well written mathematical document will be guided the main purpose of the document, but as Steenrod (1973) points out, there are two aspects to this, the formal and the informal ones. The formal side of the main purpose consists of the main mathematical statements, called (main) theorems, that document is trying to prove while the informal aspect pertains to the relevance of this mathematics to the wider scope of human endeavour. Consequentially, these aspects lead to separate structuring consideration which we now explore.
2.2.1 Formal Structure
¶ 24 Leave a comment on paragraph 24 0 As mentioned above, the mode of reasoning in mathematics is deductive logic. Theoretically, any logical deduction of a statement, which is called a proof of that statement, can be written as a linear sequence of statements. Hence, it is common to find proofs presented in this way (Alibert & Thomas, 1991). The following proof from Pillay and Ziegler is an example of such a linear presentation.
¶ 25 Leave a comment on paragraph 25 0 “Lemma 3.4. Let be a differentially closed field. Let be a -module of . Then is defined over .
¶ 26 Leave a comment on paragraph 26 0 Proof. Note that is precisely . By 3.1, we can find which form a basis for over . So is isomorphic to over . As each , is already defined over ” (Pillay & Ziegler, 2003, p. 585)
¶ 27 Leave a comment on paragraph 27 0 This linear structure is not a universal rule and often mathematicians re-arrange the order of statements within a proof for what is perceived as better exposition (Roe, 1978; Konior, 299). In such cases Konior identifies examples of the use of certain linguistic and paralinguistic signals used in mathematics texts to assist readers on how to structure their reading. For example, ‘It remains to be shown that…” to alert the reader that a previously unproved statement that was used is now going to be proved. Another example, given from Konior is ‘Whence formula (36) follows’ to signal that an earlier unproved statement is now proved.
2.2.1.1 Wider Formal Structure
¶ 28 Leave a comment on paragraph 28 0 Mathematical literature tend to prove several smaller statements (which are called ‘theorems’, ‘lemmas’, ‘propositions’ depending on their gravity) before proving the main theorem(s) (Steenrod, 1973). These smaller propositions are used to prove the main theorem(s). This is done for various reasons. One of which is to increase the readability by breaking down large proofs into smaller ones. It is also the case that before certain statements the author may like to make certain informal comments or need to define a concept for the following statements to be made.
¶ 29 Leave a comment on paragraph 29 0 Steenrod brings the organisation of these smaller statements into focus; since these statements become a part of the proof of main theorem, similar considerations arise for the sequencing of these statements as they do for the structuring of an individual proof. As he points out, there may be more than one way of ordering the propositions leading to the main theorem and that some orders and structures of statements may provide greater clarity than others. Thus the order is a point of careful consideration for the writer. The order of these statements should reflect an organic thinking process that leads to the main theorem.
¶ 30 Leave a comment on paragraph 30 0 It is customary in mathematics to signal and label a theorem, proof or definition with a mini-heading. This clarifies to the audience what kind of idea is to follow and allows the author to easily reference the idea at another point in the text. For example, in Pillay and Ziegler’s lemma (and its proof) quoted above, the headings “Lemma 4.2” and “Proof” distinguish between the statement being made and its proof. The enumeration included in the heading of the Lemma allows for easy referencing of definitions, lemmas, theorems. We can see this in Pillay and Ziegler’s proof of the lemma presented above, when they state, “By 3.1”. Here they are referencing a previous proposition, labelled 3.1, to justify their next claim.
2.2.2 Informal Structure: Contextual Narrative
¶ 31 Leave a comment on paragraph 31 0 Steenrod (1973) asserts that the discussion around the informal aspects should attend to the following considerations:
¶ 32
Leave a comment on paragraph 32 0
“(1) brief reviews of background material to set the stage,
(2) presentation of the motivations or leading questions,
(3) consideration of examples to derive conjectures,
(4) rough descriptions of the results to be obtained and methods to be used, and ” (Steenrod, 1973, p. 9)
¶ 33 Leave a comment on paragraph 33 1 That is to say, the manner in which the informal discussion is structured should serve to convey these points. In particular, Steenrod states that these points should be considered in the introductory section to ‘set the stage’, a thought which is echoed by Brendt (2014). However, these points can be revisited at other points in the document where appropriate.
- ¶ 34 Leave a comment on paragraph 34 0
- Methodology
¶ 35 Leave a comment on paragraph 35 1 The methodology used in this paper follows the framework of Yin’s (2011) five-phased process for qualitative research, which are Compiling, Dissembling, Resembling, Interpreting and Concluding. The compiling stage can be thought of as gathering data. The dissembling stage decomposes the data into key characteristics relevant to the research problem and then the resembling stage rearranges the data, according to these characteristics. The resembling is intended to make the data amenable to interpretation leading to a conclusion against the given research question or hypothesis. We shall firstly describe how the compiling stage was achieved in the proceeding subsection. Section 3.2 then explains how the data was deconstructed into the desired characteristics of mathematical writing, as outlined by the literature review, and then reconstructed so to be able to interpret whether students’ writing contained these characteristics.
3.1 The Sample
3.1.1 Method of Data Collection
¶ 36 Leave a comment on paragraph 36 3 The kind of data that was used was existing document data (Denscombe, 2010). More precisely, the analysis was performed on texts that students have already written as a part of homework rather than setting a new task. The benefit of analysing existing data is that the writing they produced for this homework is that this writing would have more likely been done in a natural setting. Setting a new task would have required disclosure of the purpose of the task prior to their undertaking and hence possibly influenced into their writing style. A sample of the students’ texts is given in Appendix B.
3.1.2 The Task the Pupils were asked to Complete
¶ 37 Leave a comment on paragraph 37 0 The pupils were asked to show why, if given a sample from a population, the sample mean and sample variance (i.e. and respectively) are unbiased estimators of the population mean and population variance respectively. Not only were students required to provide a mathematical proof of this but they were also asked to define the concepts that led to the proof, and to motivate the problem (i.e. state why it is important). They were also asked to explain the method they use to investigate whether these estimators are biased or not so as to link their motivation with the mathematical proof. Hence, the task elicited a wide array of mathematical writing skills for analysis. The brief for the task given to the students is given in Appendix A.
3.1.3 The Students
¶ 38 Leave a comment on paragraph 38 1 Our sample consisted of texts from eight year 13 students from a sixth form college in London. The students had not ben explicitly taught how mathematical writing whilst at the college and, as far as I am aware, they were not taught such a thing elsewhere.
¶ 39 Leave a comment on paragraph 39 0 The students that were selected for this sample have exhibited strong understanding of statistics in internal and external examinations. All students in the sample were predicted between a B and A* for their Further Mathematics A Level when the sample was taken. Also, all students achieved over 80 out of 100 UMS (standing for ‘Uniform Mark Scale’) score for their S1 paper that they sat the previous year. This score is relevant here because the task that was set comes under the topic of statistics. It seemed beneficial to analyse the writing of students with strong understanding of statistics so as to mitigate, as far as possible, mathematical misconceptions effecting their texts and to allow us to analyse their writing skills.
3.1.4 Ethics
¶ 40 Leave a comment on paragraph 40 0 According to BERA (2011) it is important that all participants of an educational research study be informed of their participation and the purpose of the study. Therefore, a letter was sent out to all participants and their parents informing of them of both of these aspects. The letter informed them of the participants’ rights with respects to this research. In particular, it informed them of their right to withdraw from the research.
¶ 41 Leave a comment on paragraph 41 0 3.2 Dissembling and Resembling: Analysing Texts
¶ 42 Leave a comment on paragraph 42 0 The texts were analysed for the qualities of written mathematics outlined in the literature review. In linguistic terminology, this was a corpus analysis (i.e. an analysis of the characteristics a collection of pieces of text) on a sample of students’ writing (Bhatia, 1993; Hyland, 2013). To do this, an assessment rubric was created which attempted to crystallised the characteristics mentioned in the literature review. To create this rubric, writing characteristics were divided into two main categories, Language and Structure. These categories were then further sub-divided into two subgroups each, ordinary English and mathematical English within the Language category and formal structure and informal structure with the Structure category. The precise rubric is given in table 1
¶ 43 Leave a comment on paragraph 43 0 Table 1
¶ 44 Leave a comment on paragraph 44 0 The Assessment Rubric
| Characteristic | Forms of characteristic to check for |
Language |
|
Basic English |
|
| Good Spelling | n/a |
| Good Grammar | n/a |
| Clear and concise sentence structures | n/a |
Formal English |
|
| Appropriate choice of words and terms used. | · Use of appropriate technical language (see below).
¶ 45 Leave a comment on paragraph 45 0 · The words and terms that are used are of an appropriate sophistication to clearly, succinctly and fully convey meaning. ¶ 46 Leave a comment on paragraph 46 0 · Absence of colloquialisms. |
| Appropriate distance of the author and audience from the text | · The impersonal we
¶ 47 Leave a comment on paragraph 47 0 · Nominalisations ¶ 48 Leave a comment on paragraph 48 0 · Use of the imperative ¶ 49 Leave a comment on paragraph 49 0 · Passive voice (used in a way that is not awkward[1] and not overused ) |
Mathematical English |
|
| Appropriate mathematical terms are used to convey meaning and done so correctly. | · New terms are defined.
¶ 50 Leave a comment on paragraph 50 0 · Terms are referred to correctly. |
| Mathematical symbols are used in a way that is correct and support the conveyance of meaning | · (Strings of) symbols are embedded within the text (not standing alone without explanation)
¶ 51 Leave a comment on paragraph 51 0 · New symbols are defined. ¶ 52 Leave a comment on paragraph 52 0 · Symbolic manipulations are accompanied by explanations of purpose and process of manipulation. ¶ 53 Leave a comment on paragraph 53 0 · Symbols are strung together correctly. ¶ 54 Leave a comment on paragraph 54 0 · Symbolic manipulations must be clearly laid out e.g. it is advisable that algebraic manipulations go down the page with equality signs aligned. |
Structure |
|
Formal Structure |
|
| Proofs must complete and clear | · Sequencing of steps in proof must be logical.
¶ 55 Leave a comment on paragraph 55 0 · Appropriate number of steps must be given so as to make the argument clear. ¶ 56 Leave a comment on paragraph 56 0 · Symbolic content and manipulation must be explained (see above). ¶ 57 Leave a comment on paragraph 57 0 · It should be made clear what is being proved. ¶ 58 Leave a comment on paragraph 58 0 · For larger proofs there should be an indication of how it is going to be proved. |
| The sequencing of theorems in the document must be such that it aids the reader to ascertain the author’s thought process towards achieving the main result. | · Ordering of theorems, proofs and definitions must be logical.
¶ 59 Leave a comment on paragraph 59 0 · Theorems, proofs and definitions should be clearly labelled. ¶ 60 Leave a comment on paragraph 60 0 · The author should explicitly state when they are using a previous result in the document by clear referencing. ¶ 61 Leave a comment on paragraph 61 0 · Where necessary, explanation is given between theorems to explain connections between separate statements. |
Informal Structure |
|
| The purpose of the text should be explained. | The author should explicitly explain the following (preferably in the introduction):
¶ 62 Leave a comment on paragraph 62 0 · What the problem is that they are tackling. ¶ 63 Leave a comment on paragraph 63 0 · What is the motivation for studying such a problem (e.g. historical context or/and answering problems in other fields of study) ¶ 64 Leave a comment on paragraph 64 0 · The main theorem(s) that they shall prove in the text to address the main problem they mention. |
| The author should describe the method by which they will obtain their main results. | · Describe the main results that shall prove en route to the main theorem(s).
¶ 65 Leave a comment on paragraph 65 0 · Where appropriate, discuss possible alternative treatments of the problem and why the author has chosen the current approach. |
¶ 65 Leave a comment on paragraph 65 0
¶ 66 Leave a comment on paragraph 66 1 The educational level of the students was also considered when constructing the rubric. For instance, given the issues around the passive voice discussed in the literature review, some higher educational authorities may choose to omit the passive voice from the rubric entirely. However, some concession for was made here in view of the lack of experience the students had in technical writing.
3.2.1 Analysing
¶ 67 Leave a comment on paragraph 67 0 The texts were then analysed against the rubric grading the use of each feature and quality in the rubric according to the following “traffic light” grading system:
- ¶ 68 Leave a comment on paragraph 68 0
- G (for “Green)– Meaning that the characteristic is clearly present
- A (for “Amber”)– Meaning that various aspects of the characteristic are present but requires some improvement to be absolutely clear.
- R (for “Red”) – Meaning that there is a fundamental misconception of how that characteristic was used.
- X to signify the characteristic was absent from the text
¶ 69 Leave a comment on paragraph 69 1 The ‘X’ grade is included in the system because in some cases it is important to distinguish absence from a misconception. For example, the omission of nominalisations would not necessarily imply that the student misunderstands them or cannot use appropriate voicing. Where it was necessary and helpful for recording information regarding the text notes were also written alongside these grades.
¶ 70 Leave a comment on paragraph 70 0 This meant that the original data was resembled into new data recording the presence and quality of characteristics present in the text. Thus this completed the next of the five-phased process which is reassembly. Note, to protect the participants’ anonymity their names were replaced by numbers in the resembled data i.e. in the tables in the next section.
¶ 71 Leave a comment on paragraph 71 0 The resembled data (along with the raw data) allowed us to interpret how well the writing compares to the academic style because of the quantitative nature of the grading system. Upon the interpretation a conclusion was drawn identifying the similarities and differences of the students’ writing style to that of academic mathematics.
¶ 72 Leave a comment on paragraph 72 0
¶ 73 Leave a comment on paragraph 73 0
- ¶ 74 Leave a comment on paragraph 74 0
- Data Analysis
5.1 Language
Table 2
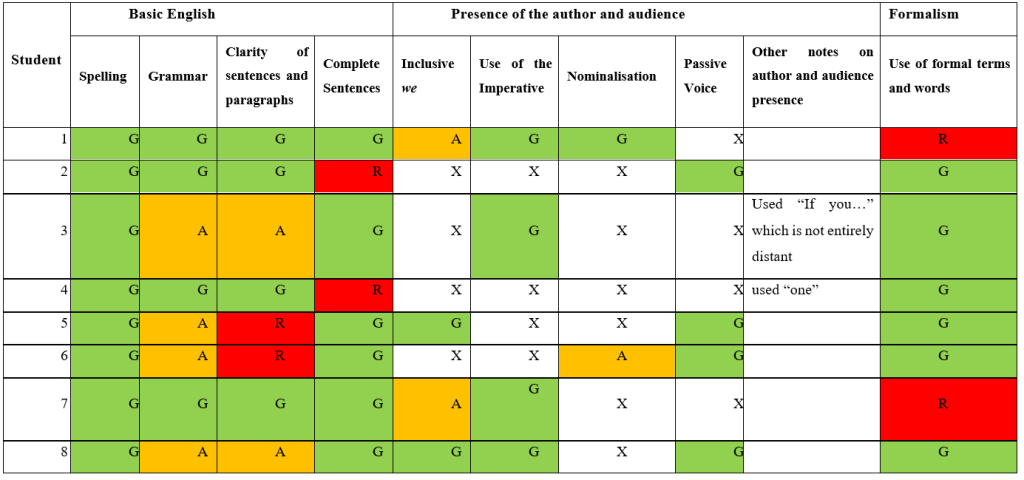
Use of Ordinary English
Interpretation:
¶ 75 Leave a comment on paragraph 75 0 Table 1 shows that most aspects of ordinary English were good with only exceptions in each subcategory of shortcomings. The basic English skills (the spelling and grammar) were well exhibited. There were only a couple of instances of poor grammar which also coincided with lack of clarity of the writing. A further strength throughout the sample is that all texts used some form of distant authorial voice.
¶ 76 Leave a comment on paragraph 76 0 Some students decided to use a greater variety of techniques for creating a distant voice and distant audience. Whichever technique they did choose they employed well. The passive voice was only ever used to say “it can be viewed”. The appropriate active variant of this would “We can view it as”. However, we can see that the active variant is one word longer, no easier to read and possibly brings unnecessary emphasis onto the actor of the verb “view” (that is, the persons doing the “viewing”). Hence, this use of the passive voice was deemed to be good. The audience presence was satisfactory in most cases except for student 3 who used ‘you’. Though this was impersonal, it is still not the appropriate engagement for the style.
¶ 77 Leave a comment on paragraph 77 0 In general, the formality in the text was also good. Along with the distant authorial voice and correct audience presence, there was, in general, a good choice of words and terms. The only exceptions to this were students 1 and 7 who both chose to use terms such as ‘When doing statistics’ in their text. However, usage of statements such as “That’s all the assumptions we need. Now let’s do some maths!” suggest that rather than misunderstanding how to write formally, they made an intentional choice to write informally to be fun. Therefore, it would be inadvisable to assess their ability to write formally based on this evidence. Indeed, the original brief the students were given did not explicitly state that the style was to be formal and hence the lack of formality in the some of the texts can be taken to be failure of the brief.
¶ 78 Leave a comment on paragraph 78 0 It should be noted that certain texts, such as those of students 2 and 4, had little written content and the writing that was there was quite terse. This means that though these students exhibited formality and appropriate voicing in what they did write, it still remains open whether they would sustain these features if they elaborated in their writing.
¶ 79 Leave a comment on paragraph 79 0
Table 3
Mathematical English
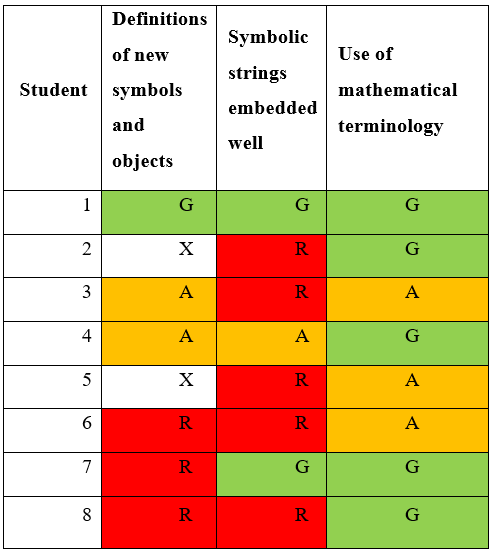 |
¶ 80 Leave a comment on paragraph 80 0
Interpretation:
¶ 81 Leave a comment on paragraph 81 0 The use of mathematical terminology was mostly good with some improper usages. These improper usages all seem tied to misunderstandings of the concepts explained. The exception to this seemed to be student 6’s usage of over when stating for a discrete random variable “the mean is equal to the sum of over every possible value weighted by the probability of the value”.
¶ 82 Leave a comment on paragraph 82 1 The embedding of the algebra was generally poor. Few defined variables and when performing manipulations, few described what manipulations they were performing. This is particularly the case in the texts that presented little writing overall (see the interpretation of the ordinary English). Such texts often neglected to explain how the assumptions were used to perform certain manipulations be seen as making their mathematics incorrect. In some cases the algebraic content were standalone units that did not interact with the rest of the text.
¶ 83 Leave a comment on paragraph 83 0
5.2 Structure
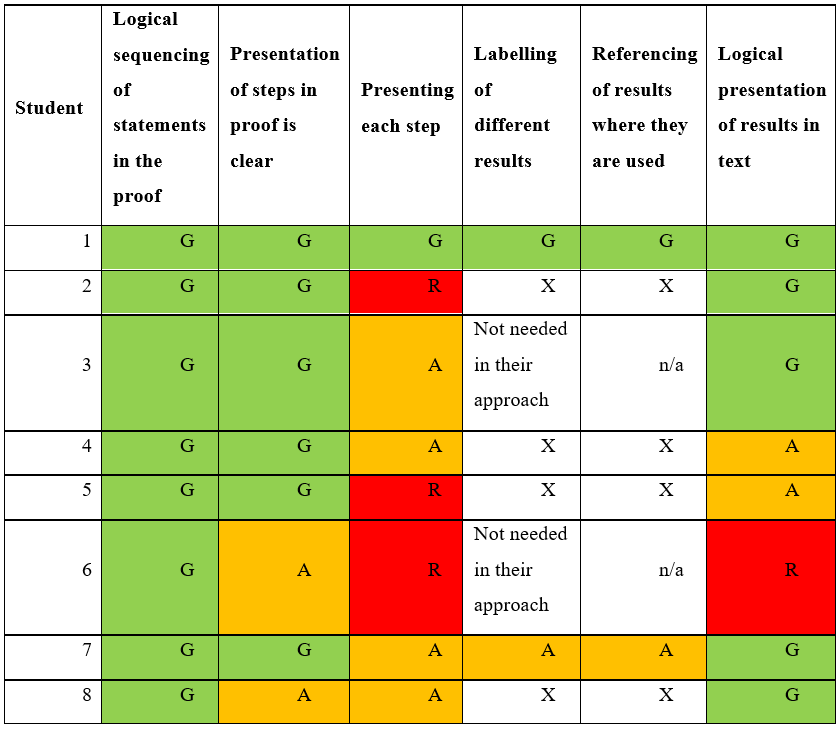
Table 4
Formal Structure
Interpretation:
¶ 84 Leave a comment on paragraph 84 0 The logical structure of all of the documents was good; the sequence of statements in the proofs clearly reflected a natural sequence of thoughts that lead to the require results. Most layouts of these steps and results was good but a few could have been improved. For instance, students 6 and 9 wrote their algebra going across the page rather than separating each manipulation with a new line and aligning equalities. A more significant issue was the lack of labelling and referencing of results which reduced the clarity of various students’ work. Not only did this mean that it was unclear what was being proved at any one given point, it also meant that when a result was used later on, this was not properly specified.
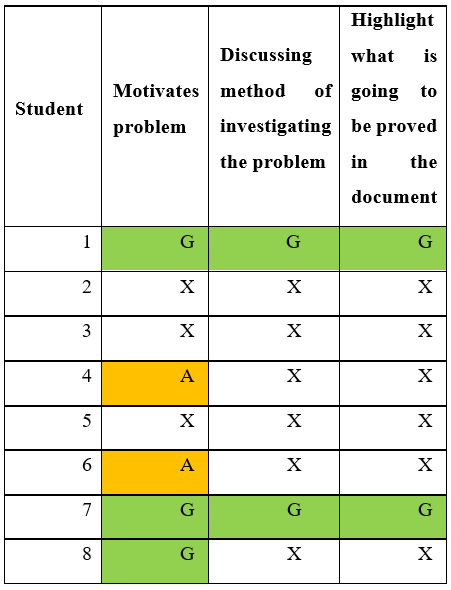
Table 5
Informal Structure
Interpretation:
¶ 85 Leave a comment on paragraph 85 0 This was perhaps the weakest of the four areas. In spite of being specifically asked to motivate the problem they were to investigate, three students failed to attempt this entirely, and only three managed to do this convincingly. Furthermore, only two of those three attempted to describe their strategy for investigate the problem and the results they were going to prove. Though it should be noted that the two that attempted this did so very well.
¶ 86 Leave a comment on paragraph 86 0
- ¶ 87 Leave a comment on paragraph 87 0
- Conclusion
¶ 88 Leave a comment on paragraph 88 0 The analysis shows that the students’ writing reflects the formality of academic mathematical writing very well. Most of the students created an appropriate distance between the persons participating (i.e. the author and the audience) and the actions of the text, often by choosing only one or two techniques for creating this distance but employing them well.
¶ 89 Leave a comment on paragraph 89 0 The students were also provide a formal structure to their documents. Their proofs were laid out in a logical and sequential manner, aiding the readers understanding of the reasoning process being presented.
¶ 90 Leave a comment on paragraph 90 1 However, a striking difference between the students’ text and that of academic writing is the amount of ordinary English. The students’ text generally exhibited far less explanation and description of their mathematics than would be expected in written mathematical discourse. There was often no commentary alongside their algebraic work to elucidate their thinking to the audience, poor referencing of previous mathematical results being used and a stark lack of informal discussion. This is quite possibly a by-product of the way algebra (and mathematics as a whole) is traditionally taught which is as a string of symbolic manipulations devoid of any descriptive writing (Baroody & Ginsburg, 1990; Morgan, 1998). A consideration for future research may be to consider if this a more general phenomena among mathematics students, and if so, why. We can also ask what strategies would help students produce more cohesive and well explained texts. We shall discuss this point further in the next section.
¶ 91 Leave a comment on paragraph 91 0
- ¶ 92 Leave a comment on paragraph 92 0
- Evaluating Comments and Further Research
7.1 Combining with Assessment for Learning Strategies to improve Formal Writing
¶ 93 Leave a comment on paragraph 93 0 As discussed in the introduction, Santos and Semana (2014) found that using assessment for learning (AfL) strategies with students’ written mathematics helped improve the clarity of mathematical explanations. AfL can be understood elicitation of the students understanding upon which a teacher makes decisions on how to proceed with their teaching. As a part of Santos and Semana’s AfL strategy they also produced a rubric to assess the quality of written mathematics. However, this rubric focused on depth (i.e. how much they explained) and clarity of informal mathematical writing. This raises the question whether using similar AfL strategies with the rubric presented here can lead to improved formal mathematical writing. Santos and Semana’s work suggests that such strategies should help improve the level of explanation in student texts. Therefore, it seems likely that such strategies would also help develop the cohesiveness of student texts e.g. merge text with algebraic work.
7.2 Writing a Tool for Learning
¶ 94 Leave a comment on paragraph 94 0 There is a large body of research that suggests writing can be used as a learning tool in mathematics (e.g. see Baroody & Ginsburg, 1990; Borasi & Rose, 1989; Pugalee, 2004; Pugalee, 2001). In particular, a study by Pugalee (2004) indicated that writing supports problem solving skills because it serves as metacognative framework for the student. In other words, writing thoughts make them apparant to the student and hence, more amenable to self-critique. Since the rubric here is intended, at least in part, to identify clear mathematical written communication, could this rubric be used in conjunction with writing strategies suggested by Pugalee to further enhance problem solving skills? More precisely, could this rubric be used with AfL strategies similar to those of Santos and Semana (2014) to enhance such skills?
7.3 Critiquing the Rubric and Grading System
¶ 95 Leave a comment on paragraph 95 0 It is feasible to think that the rubric and grading system could be used by educators in their teaching practice. Before such an implementation, it may be advisable to review the rubric and grading system since there are aspects of the grading system that maybe somewhat difficult to manage in day-to-day teaching usage. For instance, there could be confusion around the meaning of the X grade; in some cases the absence of a technique had no negative impact so long as another appropriate technique was used (e.g. authorial voicing) and others where the absence had a significant impact (such as the informal structural matters). Moreover, some of the qualities could not receive an X which may have added confusion to someone trying to interpret the grids. Also, the grading system produces quite a large string of data for one text. This could quickly become unmanageable if it is used with a large group of students. Hence, for any further use of the rubric or grading system one may wish to consider streamlining it first.
7.4 The Task given to the Students
¶ 96 Leave a comment on paragraph 96 0 The writing produced by the students was clearly heavily influenced by the task and how it was presented. This leads to the following two questions:
- ¶ 97 Leave a comment on paragraph 97 0
- Would a different task produce different results?
- Would a different presentation of the current task produce different results?
¶ 98 Leave a comment on paragraph 98 0 A task that required different mathematical techniques may, indeed, produce different results. The proof involved in the current task was quite algebraic in nature. Considering algebra has traditionally been taught with very little description to accompany the manipulations (Nardi & Steward, 2003; Baroody & Ginsburg, 1990), one may wish to consider a task which was not algebraic at all. Also, one could attempt a task that would require some other desirable features to be included in the writing such as a conclusion discussing historical connections to other work and further questions that can be asked about the mathematics presented in the text (Steenrod, 1973; Krantz, 2007).
¶ 99 Leave a comment on paragraph 99 1 The analysis of the students’ text would suggest that the manner in which this task was presented in the brief did impact the students’ output. For instance, though the brief implied that the text needed to be formal, it did not explicitly say so. As such, some students seem to have taken this as licence to use some informal language. Furthermore, it can be argued that the task brief could place more emphasis on motivating the problem and describing the method of addressing it. Hence, it can be investigated whether improvements are seen in students writing if the task were re-worded to explicitly mention these.
¶ 100 Leave a comment on paragraph 100 0
- ¶ 101 Leave a comment on paragraph 101 0
- 8. References
¶ 102 Leave a comment on paragraph 102 0 Alibert, D. & Thomas, M., 1991. Research on Mathematical Proof. In: D. Tall, ed. Advanced Mathematical Thinking. Dordrecht: Kulwe Academic Publishers, pp. 215 – 230.
¶ 103 Leave a comment on paragraph 103 0 Baroody, A. J. & Ginsburg, H. P., 1990. Chapter 4: Children’s Mathematical Learning: A Cognitive View. Journal for Research in Mathematics Education, Volume 2, pp. 51-64+195-210.
¶ 104
Leave a comment on paragraph 104 0
BERA, 2011. Ethical guidelines for educational research. [Online]
Available at: http://content.yudu.com/Library/A2xnp5/Bera/resources/index.htm?referrerUrl=http://free.yudu.com/item/details/2023387/Bera
[Accessed 18 March 2016].
¶ 105 Leave a comment on paragraph 105 0 Bhatia, V. K., 1993. Analysing Genre: Langauge Use in Professional Settings. Harlow, UK: Pearson Education.
¶ 106 Leave a comment on paragraph 106 0 Borasi, R. & Rose, B. J., 1989. Journal writing and mathematics instruction. Educational Studies in Mathematics, 20(4), pp. 347-365.
¶ 107
Leave a comment on paragraph 107 0
Brendt, B. B., 2014. How to write mathematical papers. [Online]
Available at: http://www.math.uiuc.edu/~berndt/writingmath.pdf
[Accessed 06 08 2016].
¶ 108 Leave a comment on paragraph 108 0 Britton, J., 1970. Language and learning. Portsmouth, New Hampshire: Boynton/Cook.
¶ 109 Leave a comment on paragraph 109 0 Britton, J. et al., 1975. The development of writing abilities. In: London: Macmillan, pp. 11-18.
¶ 110 Leave a comment on paragraph 110 0 Chapman, A., 1997. Towards a model of language shifts in mathematics learning. Mathematics Education Research Journal, 9(2), pp. 152-173.
¶ 111 Leave a comment on paragraph 111 0 Denscombe, M., 2010. The Good Research Guide. 4th ed. Maidenhead, UK: Open University Press.
¶ 112 Leave a comment on paragraph 112 0 Dye, R., 1991. Hexagons, Conics, A5 and PSL2 (K). Journal of the London Mathematical Society, s2-44(2), pp. 270-286.
¶ 113 Leave a comment on paragraph 113 0 Emig, J., 1971. The composing processes of twelfth graders. Urbana, Illinois: NCTE.
¶ 114 Leave a comment on paragraph 114 0 Ervynck, G., 1992. Mathematics as a foreign language. Proceedings of the Sixteenth Conference of the international Group for the Psychology of Mathematics Education, Volume 3, pp. 217-233.
¶ 115 Leave a comment on paragraph 115 0 Gee, J. P., 2011. An Introduction to Discourse Analysis. 3rd ed. Oxon: Routledge.
¶ 116 Leave a comment on paragraph 116 0 Gillman, L., 1987. Writing Mathematics Well: A Manual for Authors. s.l.:The Mathematical Association of America.
¶ 117 Leave a comment on paragraph 117 0 Halliday, M., 1975. Some aspects of sociolinguistics. Copenhagen: UNESCO.
¶ 118 Leave a comment on paragraph 118 0 Halliday, M. A. K. & Martin, J. R., 1993. Writing Science: Literacy snf Discursive Power. London: Falmer Press.
¶ 119 Leave a comment on paragraph 119 0 Halmos, P. R., 1975. How to write mathematics. In: N. E. Steenrod, P. R. Halmos, M. M. Schiffer & J. A. Dieudonne, eds. s.l.:American Mathematical Society.
¶ 120 Leave a comment on paragraph 120 0 Higham, N., 1998. Handbook of Writing for the Mathematical Sciences. 2nd ed. Philadelphia: SIAM.
¶ 121 Leave a comment on paragraph 121 0 Hyland, K., 2013. Teaching and Researching Writing. 2nd ed. Abingdon, UK: Taylor and Francis.
¶ 122 Leave a comment on paragraph 122 0 Johnsson, R., 2003. Case Study Methodology. Stockholm, s.n.
¶ 123 Leave a comment on paragraph 123 0 Kane, R. B., 1967. The readability of mathematical english. Journal of Research in Science Teaching, 5(3), pp. 296-296.
¶ 124 Leave a comment on paragraph 124 0 Knuth, D., 1985. Algorithmic thihnknign and mathematical thinking. American mathematical monthly, Volume 92, pp. 170-181.
¶ 125 Leave a comment on paragraph 125 0 Knuth, D. E., Larrabee, T. & Roberts, P. M., 1989. Mathematical Writing. s.l., s.n.
¶ 126 Leave a comment on paragraph 126 0 Konior, J., 299. Research into the construction of mathematical texts. Educational studies in mathematics, Volume 24, pp. 251-256.
¶ 127 Leave a comment on paragraph 127 0 Krantz, S. G., 1996. A Primer of Mathematical Writing: Being a Disquisition on Having Your Ideas Recorded, Typeset, Published, Read & Appreciated. Providence: American Mathematical Society.
¶ 128 Leave a comment on paragraph 128 0 Krantz, S. G., 2007. How to write your first paper. Notices of the American Mathematical Society, 54(11), pp. 1507-1511.
¶ 129 Leave a comment on paragraph 129 0 Lave, J. & Wenger, E., 1991. Situated learning: Legitimate peripheral participation. Cambridge: Cambridge University Press.
¶ 130 Leave a comment on paragraph 130 0 Lea, M. R. & Street, B. V., 2010. The “academic literacies” model: Theory and application. Theory into Practice, 45(4), p. 368–377.
¶ 131 Leave a comment on paragraph 131 0 Morgan, C., 1998. Writing mathematically: The discourse of investigation. London: Taylor and Francis.
¶ 132 Leave a comment on paragraph 132 0 Nardi, E. & Steward, S., 2003. Is Mathematics T.I.R.E.D? A Profile of Quiet Disaffection in the Secondary Mathematics Classroom. British Educational Research Journal, 29(3), pp. 345-367.
¶ 133 Leave a comment on paragraph 133 0 Ofsted, 2013. Improving literacy in secondary schools: a shared responsibility, Manchester: Ofsted.
¶ 134 Leave a comment on paragraph 134 0 Pillay, A. & Ziegler, M., 2003. Jet spaces of varieties over differential and difference fields. Selecta Mathemtica, 9(4), pp. 579-599.
¶ 135 Leave a comment on paragraph 135 0 Pimm, D., 1984. Who is we?. Mathematics Teaching, Volume 107, pp. 39-42.
¶ 136 Leave a comment on paragraph 136 0 Pimm, D. K., 1987. Speaking Mathematically: communication in mathematics classsrooms. London: Routledge &Kegan Paul Ltd.
¶ 137 Leave a comment on paragraph 137 0 Pugalee, D., 2001. Writing, mathematics, and metacognition: looking for connections through students’ work in mathematical problem solving. School Science and Mathematics, 101(5), pp. 236-245.
¶ 138 Leave a comment on paragraph 138 0 Pugalee, D. K., 2004. A comparison of verbal and descriptions of students’ problem solving processes. 55(1/3), pp. 27-47.
¶ 139
Leave a comment on paragraph 139 0
Reiter, A., 1995. Writing a Research Paper in Mathematics. [Online]
Available at: http://web.mit.edu/jrickert/www/mathadvice.html
[Accessed 1 08 2016].
¶ 140 Leave a comment on paragraph 140 0 Roe, P., 1978. Scientific Text: selections from the linguistic evidence presented in a study of difficulty in science text-book.. Birmingham: University of Birmingham, English Language Research.
¶ 141 Leave a comment on paragraph 141 0 Rounds, P., 1987. Multifunctional personal pronoun use in an educational setting. English for Sepcific Purposes, 6(1), pp. 18-29.
¶ 142 Leave a comment on paragraph 142 0 Santos, L. & Semana, S., 2014. Developing maathematics written communication through expository writing supported by assessment strategies. Educational Studies in Mathematics, 88(1), pp. 65-87.
¶ 143 Leave a comment on paragraph 143 0 Steenrod, N. E., 1973. How to write mathematics. In: N. E. Steenrod, P. R. Halmos, M. M. Schiffer & J. A. Dieudonne, eds. How to write mathematics. s.l.:American Mathematical Society.
¶ 144 Leave a comment on paragraph 144 0 Strube, P., 1989. The notion of style in Physics texbooks. The journal for research in science teaching, 26(4), pp. 291-299.
¶ 145 Leave a comment on paragraph 145 0 Yin, R., 2011. Qualitative Data from Start to Finish. 1st ed. New York: Guildford Press.
¶ 146 Leave a comment on paragraph 146 0 Yin, R., 2014. Case Study Research: Design and Methods. Fifth ed. California, USA: SAGE Publications.
¶ 147 Leave a comment on paragraph 147 0
¶ 148 Leave a comment on paragraph 148 0
¶ 149 Leave a comment on paragraph 149 0
¶ 150 Leave a comment on paragraph 150 0
¶ 151 Leave a comment on paragraph 151 0 Appendix A: Task Brief
¶ 152 Leave a comment on paragraph 152 0 The brief given to the students is given the green box.
¶ 153 Leave a comment on paragraph 153 0
¶ 154
Leave a comment on paragraph 154 0

Appendix B: Examples of Student Texts
¶ 155 Leave a comment on paragraph 155 0 Note that the teacher’s feedback is in green.
¶ 156 Leave a comment on paragraph 156 0 Figure B1: Text form student 1
¶ 157
Leave a comment on paragraph 157 0

¶ 158 Leave a comment on paragraph 158 0 Figure B2: First page of work from student 3
¶ 159
Leave a comment on paragraph 159 0

¶ 160 Leave a comment on paragraph 160 0 Figure B3: Second page of work from student 3
¶ 161
Leave a comment on paragraph 161 0

¶ 162 Leave a comment on paragraph 162 0 Figure B4: First page of work from student 7
¶ 163 Leave a comment on paragraph 163 0 [1] See the literature review for what is meant by an “awkward” use of the passive voice
¶ 164 Leave a comment on paragraph 164 0 [2] In the original text there was a typo here and read “After formalise”


I think the Abstract is very well written and very easy to follow. The only thing that confused me a little bit is it doesn’t much define the context of the study. You refer to A-level students but you do not mention which context of instruction (Europe, Asia …etc) Especially with literacy there is a cultural element that is attached that is usually specific to the context. Maybe if you could just add A level students in British school for instrance